Was ist Gradient Descent und wie funktioniert es?
(dieser Beitrag basiert lose auf dem von fastai zur Verfügung gestellten fastbook)
Dieser Blog Post ist nicht dafür gedacht aufzuzeigen, wie die mathematische Berechnung hinter Gradient Descent funktioniert. Denn zum Glück gibt es genau dafür Computer, die das Ganze wahrscheinlich millionenfach schneller berechnen können als wir. Ich will eine intuitive Erklärung für Gradient Descent liefern, wofür wir Gradient Descent überhaupt brauchen und wie wir mit simplen Python Code unseren eigenen auf Gradient Descent beruhenden Algorithmus bauen können.
Ich erinnere mich, dass ich zu Schulzeiten (und mehr als Abi-Mathe wird für diesen Post wahrhaftig nicht gebraucht) die Ableitungsregeln gelernt und auf Funktionen angewandt habe, aber wirklich Sinn und Zweck habe ich in dem Ganzen nie gesehen. Im besten Fall hat sich die Lehrerin einen an den Haaren herbeigezogenen Fall ausgedacht, um nicht einfach stumpf die Funktion zu liefern, die abgeleitet werden soll. Ich hoffe nach diesem Blog wird klarer, weswegen Ableitungen bzw. die dazugehörigen Gradienten doch eine ziemlich coole und nützliche Sache sind.
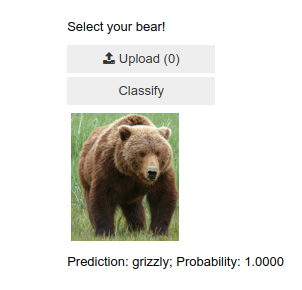
Zunächst einmal möchte ich zeigen, was Gradient Descent kann:
Ein Algorithmus, der erkennen kann, was für ein Bär auf einem gegebenem Bild zu sehen ist? Was zur Hölle hat das mit Gradient Descent zu tun? Wenn du es bis zum Ende des Posts aushältst, wirst du das hoffentlich verstehen.
Gradient Descent hilft Computern dabei zu lernen. Das Ganze sollten wir uns vielleicht in einem Schaubild einmal näher anschauen:
Die Idee ist dabei wie folgt: Wir haben ein Modell, welches anhand von Bildern erkennen soll, welche Art von Bär hier zu sehen ist. Nachdem wir genügend Bilder von verschiedenen Bären gesammelt haben, fangen wir an unser Modell zu fragen, was es glaubt für eine Art von Bären zu sehen (predict). Wir können uns nun Metriken überlegen, an denen wir erkennen können, wie gut diese Vorhersage unseres Modells ist, zum Beispiel wie häufig das Modell die richtige Bärenart vorhergesagt hat und wie häufig es falsch lag. Wir können daraus einen sogenannten Loss berechnen, was nichts anderes ist als das, was die Lehrer uns immer als Funktion beschrieben haben. Wir haben also eine Funktion die uns angibt, wie gut/schlecht unser Modell Bärenarten vorhersagen kann. Diese Funktion kann zum Beispiel eine simple quadratische Funktion sein, sie kann aber theoretisch jede nur erdenkliche Form annehmen.
Wir wollen unseren Loss minimieren, sprich unsere Funktion soll so gut wie es nur kann die Funktion lernen, wie es möglichst gut Bärenarten voneinander unterscheiden kann. Lass uns eine Sekunde darüber nachdenken. Wir benutzen eine Loss-Funktion, damit wir unserem Modell Feedback geben, wie gut/schlecht es die bisherige Aufgabe gelöst hat. Mithilfe dieser Loss-Funktion lernt unser Modell, die verschiedenen Bärenarten besser zu unterscheiden. Doch wie "lernt" das Modell? Hier kommt Gradient Descent ins Spiel.
Der Gradient, also die Ableitung, gibt uns an, um wie viel die Funktion größer wird, wenn wir (optisch gesprochen) einen kleinen Schritt nach rechts bzw. einen kleinen Schritt nach links gehen von dem Punkt, an dem wir uns gerade befinden. Dies ist die Steigung von dem Punkt, an welchem wir uns gerade befinden. Doch was bringt uns das?
Ich hoffe, du hast einen Moment darüber nachgedacht. Was wir wollen, ist möglichst gut die Bärenarten voneinander zu unterscheiden. Dies steuern wir über unsere Loss-Funktion. Und je geringer unsere Loss-Funktion, desto besser sind wir im Vorhersagen, was für eine Bärenart wir hier gerade haben. Durch den Gradienten wissen wir, in welche Richtung wir uns bewegen müssen, um unsere Loss-Funktion kleiner zu machen.
Noch mag das Ganze recht abstrakt klingen, schon in Kürze folgt hier das Beispiel in Python. Ich will das Ganze aber noch einmal zusammenfassen. Wir wollen etwas optimieren, zum Beispiel möglichst genau die Bärenart vorhersagen. Um diese Funktion zu optimieren, brauchen wir die Loss-Funktion, die uns angibt, wie gut/schlecht unser Modell/unsere Zielfunktion performt. Diese Funktionen können jegliche erdenkliche Formen annehmen. Dem Gradienten ist dies jedoch egal. Der Gradient kann uns zu jedem Ort, an welchem wir uns in der Funktion befinden sagen, was mit unser Loss-Funktion passiert, wenn wir uns ein kleines Stück in eine beliebeige Richtung bewegen. Dies nutzen wir als Feedback, um die Parameter der Zielfunktion so anzupassen, dass die Loss-Funktion kleiner wird, wir also besser die Bärenarten voneinander unterscheiden können.
Dies sind die Schritte, die in dem Schaubild erklärt sind: wir initialisieren die Werte unserer Zielfunktion (anfangs zufällig, weil wir nicht wissen, wie die richtige Funktion aussieht), wir lassen unser Modell Vorhersagen treffen, berechnen daraufhin den Loss und die dazugehörigen Gradienten, um dann durch die Gradienten die Parameter des Modells anzupassen. Diesen Prozess wiederholen wir solange, bis wir mit dem Endergebnis zufrieden sind .Dies sollte auf einem sogenannten Validierungs-Set festgelegt werden, also auf Bildern von Bären, die unser Modell im Trainingsloop nicht sieht. Vielleicht wäre es hier angebracht einmal darüber nachzudenken, warum wir nicht einfach den Trainingsloop solange wiederholen, bis wir alle Bärenarten durch Gradient Descent korrekt vorhersagen können (Stichwort: Overfitting).
Genug geredet, jetzt wollen wir das Ganze auch in Code sehen!
Wir wollen mit Hilfe des oben beschriebenen Prozesses eine Funktion finden, die möglichst genau den Verlauf folgender Funktion beschrieben kann:
import torch
import matplotlib.pyplot as plt
x = torch.arange(-5,20).float(); x
y = 0.75*(x-4)**2 + 0.5*x + 1
plt.scatter(x,y);
Was wir wollen ist die Parameter dieser Funktion zu schätzen. Vom ansehen der Daten können wir bereits auf die funktionale Form schließen - ein Polynom 3ten Grades. Was wir an diesem Beispiel schon erkennen können ist, dass die angenommene Zielfunktion eine große Rolle spielt. Hätten wir von den Daten auf eine quadratische Funktion geschlossen, würden wir die "wahre" Form der Funktion nie richtig bestimmen können. Deep Learning überkommt dieses "Problem", indem es jede nur erdenkliche Funktion annehmen kann (dazu mehr in einem späteren Post).
def f(x, params):
a,b,c,d = params
return a*(x-b)**2 + (c*x) + d
Jetzt benötigen wir noch unsere Loss-Funktion (und ich hoffe hier wird klar, wie Loss-Funktion und Zielfunktion miteinander "kommunizieren"):
def mse(preds, targets): return ((preds-targets)**2).mean()
params = torch.randn(4).requires_grad_()
params
Wir starten unsere Vorhersagen:
preds = f(x, params)
plt.scatter(x,preds.detach().numpy())
Wie gut sehen unsere Vorhersagen aus?
def show_preds(preds, ax=None):
if ax is None: ax=plt.subplots()[1]
ax.scatter(x, y)
ax.scatter(x, preds.detach().numpy(), color='red')
ax.set_ylim(-10,100)
ax.set_xlim(-5,20)
show_preds(preds)
Wow! Ziemlich miserabel. Wie miserabel zeigt uns unser loss.
loss = mse(preds, y)
loss
Auf geht's Gradient! Zeig uns, wie wir unsere Parameter updaten müssen, damit der Loss kleiner wird.
loss.backward()
params.grad
Dann lass uns unsere Paramter anpassen (wir multiplizieren den Gradienten mit der sogenannten Learning Rate, dazu in einem weiteren Blog Posts mehr).
lr = 1e-5
params.data -= lr * params.grad.data
params.grad = None
params
Ist unser Loss geringer geworden?
preds = f(x,params)
mse(preds, y)
show_preds(preds)
Zum Glück ja.
Wir wollen die steps wiederholen, sodass wir langsam und mithilfe von Gradient Descent unsere Zielfunktion finden.
def apply_step(params, prn=True):
preds = f(x, params)
loss = mse(preds, y)
loss.backward()
params.data -= lr * params.grad.data
params.grad = None
if prn: print(loss.item())
return preds
lr=1e-5
for i in range(20): apply_step(params)
_,axs = plt.subplots(1,6,figsize=(24,3))
for ax in axs: show_preds(apply_step(params, False), ax)
plt.tight_layout()
Wie man sieht, passt sich die rote Kurve, also unsere Vorhersagen, immer mehr der wahren Kurve an. Alles aufgrund von Gradient Descent! Und genau diese Technik und diese Schritte, die hier in diesem Blog Post aufgezeigt wurden, sind auch die Schritte, die dabei helfen, Neuronale Netze zu trainieren. Die dann wiederum Bären auseinander halten können.
Ich hoffe, durch diesen Post ist die Idee hinter Gradient Descent ein wenig greifbarer geworden und der Sinn und Zweck von Ableitungen könnte von einer anderen Seite vielleicht ein wenig verständlicher betrachtet werden.
Bleibt dran für die nächsten Posts!
Euer Lasse